




Стеклянные линзы для уличных светильников COB обладают множеством преимуществ, которые делают их оптимальным выбором для городского освещения. Высокая прозрачность (более 90%) превышает показатели пластиковых аналогов, обеспечивая максимальную передачу света и снижая энергопотребление. Изготовленные из материалов высокого боросиликата, они отличаются исключительной термостойкостью: выдерживают температурные колебания от -40°C до 80°C, что исключает растрескивание и разрушение при резких изменениях погодных условий. Еще одна важная характеристика — устойчивость к УФ-лучам, загрязнениям, кислотным дождям и соленой влаге, что обеспечивает срок службы до 10 лет и более, сокращая расходы на обслуживание. Точность распределения светового потока (с углами освещения от 120° до 150°) исключает рассеянное свечение, снижая световое загрязнение и улучшая дорожную безопасность. К тому же, аэродинамичный дизайн способствует эффективному отводу тепла, защищая чип COB от перегрева и поддерживая стабильную работу в долгосрочной перспективе. Все эти качества делают стеклянные линзы незаменимым решением для современного городского освещения.
Еще одна важная характеристика — устойчивость к УФ-лучам, загрязнениям, кислотным дождям и соленой влаге, что обеспечивает срок службы до 10 лет и более, сокращая расходы на обслуживание. Точность распределения светового потока (с углами освещения от 120° до 150°) исключает рассеянное свечение, снижая световое загрязнение и улучшая дорожную безопасность. К тому же, аэродинамичный дизайн способствует эффективному отводу тепла, защищая чип COB от перегрева и поддерживая стабильную работу в долгосрочной перспективе. Все эти качества делают стеклянные линзы незаменимым решением для современного городского освещения.
Хотя теоретически аферрические поверхности могут иметь самые разные формы, аферрические линзы часто проектируются с поверхностями вида:
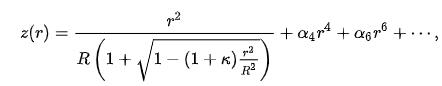
где предполагается, что оптическая ось лежит в направлении z, а z(r) — сагитта (компонента z смещения поверхности от вершины на расстоянии r от оси). Коэффициенты αn описывают отклонение поверхности от осевым симметричной квадрической поверхности, определенной R и κ. Если все коэффициенты αn равны нулю, то R — радиус кривизны, а κ — коническое число, измеренные в вершине (где r=0). В этом случае поверхность имеет форму вращения конической секции вокруг оптической оси, форма которой определяется κ:



